2025.02.03 - [재료탄소성학] - 재료탄소성학 [5] 3차원적 변형(Bulk Modulus)
재료탄소성학 [5] 3차원적 변형(Bulk Modulus)
2025.02.03 - [재료탄소성학] - 재료탄소성학 [4] True stress/strain, Engineering Stress/Strain 재료탄소성학 [4] True stress/strain, Engineering Stress/Strain2025.02.02 - [재료탄소성학] - 재료탄소성학 [3] Elastic, Work Hardening
mayunchem.tistory.com
Elastic Modulus는 Atomic Level에서의 스프링 constant와 연관지어 설명할 수 있다,

이때 S는 스프링 constant이다.

이러한 S값은 이전에 언급했다싶이, 물질이 가해지는 힘에 변형을 저항하는 정도라 생각할 수 있으므로, 가장 강한 결합인 공유결합에서 가장 큰 값을 가지고 폴리머에서 상대적으로 작은 값을 가진다.
이 개념에서 더 나아가 인접한 atom들간의 전체 위치 Energy에 대한 값을 알아보자.
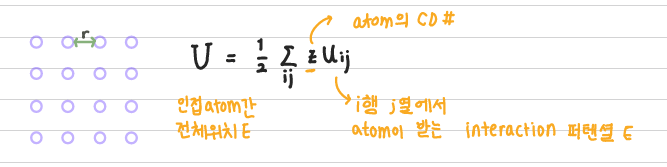
z는 원자들을 둘러싼 atom들의 coordination number를, U_ij는 i행 j열에서 원자가 받는 interaction potential Energy값이다.
이때, 이 U 값을 거리(=r)에 대한 함수로 표현할 수 있을까?
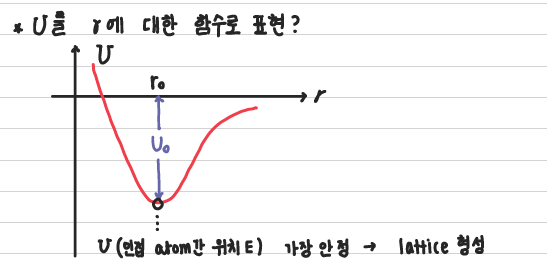
그렇다. U를 r에 대한 함수로 표현해보면 한번쯤 본적있는 그래프가 보인다.
r= r0에서 U값이 가장 작은 값을 보이며 이때의 전체 위치 에너지가 가장 낮기 때문에 r= r0일때 격자를 형성하는 것을 확인할 수 있다. 또한, r이 커지게 되면 free electron(자유전자)와 사실상 같은 상태가 된다.
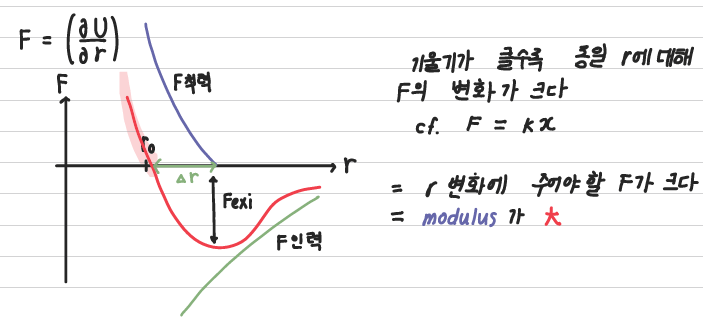
이제 이 U의 값을 r에 대해 미분한 F의 꼴로 바꾸어보자.
기울기가 클수록 동일 r에 대한 F의 변화가 큰 상태이며, 즉, atom을 동일 길이 변화에 대해 F를 많이 줘야하는 (= modulus가 큰) 상태이다.
r이 매우 작은상태에서는 원자들간의 반발력이 매우 커 U가 매우 큰 아주 불안정한 상태이지만, r을 키우면 반발력이 점차 감소하는 것을 그래프를 통해 확인할 수 있다.

이번에는 r이 아닌 atom 당 Volume을 x축에 넣어보았다. 당연히 r0^3일때, U의 값이 min이 되는 것을 확인할 수 있다.
F가 아닌 3차원적 응력을 이번에는 유도해보자.

아까 말했던 기울기에서 우리는 bulk modulus(:3차원에서의 modulus)를 얻어낼수 있다.

'학교 수업 > 재료탄소성학' 카테고리의 다른 글
| 재료탄소성학 [8] Gliding/ Climbing motion (0) | 2025.02.04 |
|---|---|
| 재료탄소성학 [7] Atomic level에서의 Slip (이론 vs. 실험), Peierls & Nabarro 방정식 (0) | 2025.02.03 |
| 재료탄소성학 [5] 3차원적 변형(Bulk Modulus) (0) | 2025.02.03 |
| 재료탄소성학 [4] True stress/strain, Engineering Stress/Strain (0) | 2025.02.03 |
| 재료탄소성학 [3] Elastic, Work Hardening/ Softening (0) | 2025.02.02 |