재료탄소성학이라는 학문은, 이름부터가 굉장히 어려운 학문이다.
하지만, 쉽게 바라보자면
탄소성 = 탄성(elastic) + 소성 (plastic)
즉, 탄성 변형과 소성 변형에 관한 학문이라고 생각하면 그 이해가 쉬울 것이다.
그렇다면, 탄성과 소성변형은 각각 무엇일까?
탄성(Elastic) 변형은 재료가 구조의 변형을 기억하지 않는 변형이고
소성(Plastic) 변형은 재료가 구조의 변형을 기억하는 변형이다.

변형은 크게 1/ 2 /3차원적 변형으로 나누어볼 수 있다. 참고로, 이들은 모두 Macroscopic(거시적) 차원에서의 변형이다.
1차원적 Macro-scopic Def.
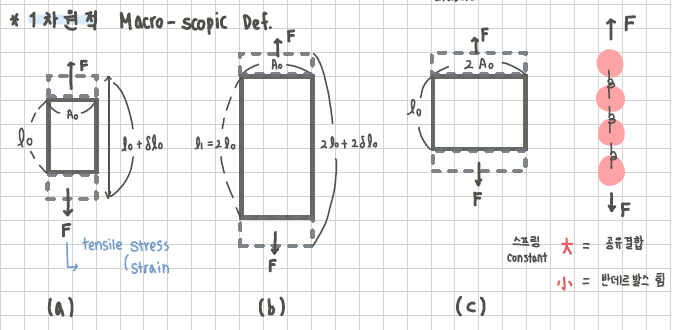
1차원적 변형의 모습을 보면 힘이 위와 아래로만 가해지고있다.
(a), (b), (c)의 변형에는 힘에 따라 길이의 변형 역시 일어나고 있다.
오른쪽의 Atom과 스프링을 통해 나타낸 그림을 보자.
Atom은 재료를 구성하는 가장 간단한 단위이다. 이들 자체는 property(특성)이 존재하지 않으나, 어떻게 붙이느냐에 따라 conductivity(전기전도도)와 같은 property의 변화가 생긴다.
Atom 사이의 연결을 스프링을 통해 나타내보았다. 만일 이 스프링 constant(상수)가 크다면 원자 사이의 결합력이 큰 공유결합과 같은 형태일 것이고, 반대로 스프링 constant가 작다면 반데르발스 힘과 같은 매우 약한 힘이 될 것이다.
그렇다면, 가한 힘(F)와 변형 길이에는 무슨 관계가 있을까?
우리는 어린 시절 용수철 저울을 써본 적이 있을 것이다. 용수철 저울은 가한 무게 즉, 힘만큼 늘어난다. 이를 쉽게 나타낸 것이 바로 훅의 법칙(Hooke's Law)이다.
훅의 법칙은 다음과 같다.
Hooke's Law(훅의 법칙); F= kx
F: 가한힘
k: (용수철) 상수
x: 변형길이
훅의 법칙은 말 그대로, 탄성체의 변형 길이(x)와 가한 힘(F)사이의 관계라고 볼 수 있다.
그래프로 나타내면 가한 힘과 변형 길이 사이의 선형적인 1차 함수 형태가 나온다.


그렇다면 우리는 이때 용수철 상수인 k를 '스프링 재료가 힘 F에 대해서 얼마나 저항하는가' 즉, 기계적인 관성이라고 볼 수 있다.
쉽게 생각해보자.
용수철 상수가 크다면 우리는 동일 힘 (F)에 대한 변형 길이 (x)가 적을 것이다. 즉, 힘에 대해 저항하는 정도가 클 것이다. 한마디로, 기계적인 관성이 클 것이다.
1차원적인 탄성 변형에도 적용이 가능할까?
우리는 그렇다면 이러한 물음을 가지게 될 것이다.
정답은 '그렇다'이다.
다만, 훅의 법칙을 직접적으로 응용하는 것이 아닌, 단위를 바꾸어 적용하게 된다.

strain(변형률)은 늘어난 길이와 원래 길이 사이의 비를 나타내며.
stress는 F(가한 힘)을 단위 면적으로 나누어준 '단위 면적 당 걸리는 힘'을 나타낸다. (dimension-less value)
또한 이때의 stress와 strain 사이의 상수를 E라고 하며, 이것을 Young's Modulus라고 한다.
Young's modulus는 재료 본연의 성질로 상수 값이며, atom의 결합력에 의해 크게 좌우되는 성질이다. 따라서, young's modulus가 크다는 것은 동일 stress에 대한 변형률이 작다는 것과 같다.
Q. 금속 결합의 Al과 ceramic ZnO의 Young's modulus를 비교하자.
Ceramic의 공유결합이 Metal의 금속 결합보다 더 강하므로, 저항 관성이 더 크다.
'학교 수업 > 재료탄소성학' 카테고리의 다른 글
| 재료탄소성학 [6] 보충) Atomic Level에서의 스프링 Constant (0) | 2025.02.03 |
|---|---|
| 재료탄소성학 [5] 3차원적 변형(Bulk Modulus) (0) | 2025.02.03 |
| 재료탄소성학 [4] True stress/strain, Engineering Stress/Strain (0) | 2025.02.03 |
| 재료탄소성학 [3] Elastic, Work Hardening/ Softening (0) | 2025.02.02 |
| 재료탄소성학 [2] 2차원적 변형, Viscoelasticity(점탄성변형) (0) | 2025.02.02 |