반도체 공학 [5] 광전 효과
반도체 공학 [4] 반도체 공학 기초 (3) Imperfection, Defect반도체 공학 [3] 반도체 공학 기초 (2) FCC, diamond structure의 Atomic Packing Factor(APK)/ Surface Density 계산반도체 공학 [2] 반도체 공학 기초 (1)반도체 공
mayunchem.tistory.com
지난 시간에는 아인슈타인의 광전 효과 실험에 대해 알아보았다. 이번 시간에는 빛의 이중성에 대해 알아보도록 하자.
빛의 입자성(m)과 파동성(λ) 사이에 연관이 있을까?
우리는 이전 시간의 광전효과를 통해 빛의 에너지와 파동성 사이의 답을 알게 되었다. 그렇다면, 입자성의 대표적인 개념인 '질량'과 파동 사이의 관계를 구할 수 있을까?
입자와 파동은 원래라면 서로 공통점을 찾을 수 없는 개념이다. 입자는 질량이 존재하고, 움직이므로 속도라는 개념도 가지지만 '운동량'이라는 개념으로 존재한다. 파동은 파장, 진동수, 진폭과 같은 '입자와 다른 개념'으로 표현된다. 드브로이는 이런 상반된 두가지 개념을 물질을 구성하는 '전자'가 가진다고 생각했다.
드브로이는 아인슈타인의 특수 상대성 이론 중 E=mc² 라는 식과 광양자 가설, 플랑크의 에너지 양자 가설에서 해답을 얻었다. 즉, 물질의 질량이 에너지이고, 파동도 에너지를 가지므로 에너지라는 중간 단계를 중심으로 관계식을 결합해 질량이 파동의 성질을 가진다는 결론을 도출한 것이다.
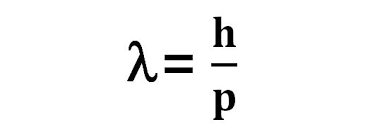
이 식을 해석하면, 모든 입자는 운동량에 반비례하는 파장을 가진다.

물질의 이중성이 중요한 이유는 무엇일까?
우리는 물질의 이중성을 통해 격자 내에서 전자가 어떻게 움직이는 지 알 수 있다.
고전 역학에서 전자 = 입자 였다.
그러나, 양자 역학에서 전자 = 파동/입자 가 된다. 파동은 주기성을 가지고, 격자도 주기성을 가지기 때문에 우리는 전자의 위치를 예측해볼 수 있다.
전자의 위치를 정확하게 알 수 있을까?

우리는 다음과 같이 파장을 const하다고 가정하거나 전자의 위치를 고정하면, 다음과 같이 전자의 위치를 정확히 특정할 수 없게 된다. 따라서, 정확하게 알 수 없지만 확률적으로는 알 수 있다. 이는 하이젠버그의 불확정성의 원리 개념과도 같다.
하이젠버그의 불확정성 원리에 대한 더 자세한 개념이 궁금하다면, 다음 링크를 참고해도 좋다.
알아두면 쓸모있는 양자역학 이야기 – 불확정성의 원리
2차 세계대전이 발발하기 몇 년 전인 1927년 제 5차 솔베이 회의에는 많은 물리학자가 참석했다. 참석한 물리학자 29명 중 무려 18명이 노벨상 수상자다. 양자역학의 큰 획을 그었던 솔베이 회의를
news.samsungdisplay.com

따라서, 에너지의 양자화, 파동과 입자의 이중성, 불확정성 원리의 개념을 토대로 슈뢰딩거 Equation을 통해 우리는 확률적으로 전자가 어디에 존재할 지 Energy band Diagram으로 알 수 있다.
슈뢰딩거 Equation은 굉장히 복잡하기 때문에 간단히 하도록 하겠다.

우리는 슈뢰딩거의 Equation의 정리를 통해 파동함수 Ψ를 구할 수 있다. 푸사이라고 읽으며, Ψ는 파동의 물리량에 대한 정보를 담고있는 시공간에 대한 함수를 의미한다. 즉, 물질을 구성하는 입자나 파동의 위치를 확률적으로 표현한 함수이자, 특정한 시간에 특정한 위치에서 입자를 발견할 확률적 크기를 의미한다.
Ψ* Ψ의 곱의 형태는 파동 밀도 함수(Probabilty Density Function)라고 한다. 이 파동 밀도 함수를 적분하게 되면 전자 발견 확률을 구할 수 있다.

삼성 디스플레이 참고자료이다.
알아두면 쓸모 있는 양자역학 이야기 - 파동함수
앞서 '양자역학 이야기 – 드브로이 물질파'에서 우리는 세상을 구성하는 요소들이 입자 뿐만 아니라 파동으로도 이루어져 있다는 것을 배웠다. 기존의 사유 방식으로는 쉽게 납득할 수 없는 개
news.samsungdisplay.com
예제로 마무리하자.
1. In 1924, de Broglie postulated the existence of matter waves. He suggested that since waves exhibit particle-like behavior, particle should be expected to show wave-like properties. The hypothesis of de Broglie was the existence of a wave-particle duality principle. The momentum of a photon is given by p = h/ λ where
λ is the wavelength of the light wave and h Planck constant. Then, de Broglie hypothesized that the wavelength of a particle can be expressed as λ= h/p where p is the momentum of the particle and λ is known as the de Broglie wavelength of the matter wave. (a) An electron has a kinetic energy of 12 meV. Determine the de Broglie wavelength (in Å), (b) a particle with mass 2.2 * 10 ^ 31 kg has a de Broglie wavelength of 112 Å. Determine the momentum and kinetic energy of the particle.
a) 드브로이의 물질파 정리를 이용한 식으로 쉽게 풀 수 있다. 에너지 단위 변환을 해준 후 플랑크 상수와 c의 값을 대입하면 되는 간단한 문제이다.

b)
에너지와 운동량 사이의 관계 식을 이용하여 쉽게 풀 수 있다.

이때, p = h/ λ 라는 식을 이용하라고 나와있으므로, p를 위 식을 통해 구할 수 있다.

The solution to Schrodinger's wave equation for a particular situation is given by Ψ(x) = sqrt (2/a0) * e^(-x/a0). Determine the probability of finding the particle between the following limits : (a) 0 ≤ x ≤ a0/4 (b) a_0 / 4 ≤ x ≤ a0 / 2, and (c) 0 ≤ x ≤ a0

파동함수 식을 통해 푸는 문제이다. 파동함수를 제곱한 후 범위에 따라 제곱하여 풀어주자.

'학교 수업 > 반도체 공학' 카테고리의 다른 글
| 반도체 공학 [5] 광전 효과 (0) | 2025.02.23 |
|---|---|
| 반도체 공학 [4] 반도체 공학 기초 (3) Imperfection, Defect (0) | 2025.02.23 |
| 반도체 공학 [3] 반도체 공학 기초 (2) FCC, diamond structure의 Atomic Packing Factor(APK)/ Surface Density 계산하기 (0) | 2025.02.20 |
| 반도체 공학 [2] 반도체 공학 기초 (1) (0) | 2025.02.20 |
| 반도체 공학 [1] 전자기학의 기초 (1) 전하, 전류, 전자기장, 전위, 저항, 이동도 (0) | 2025.02.20 |