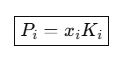재료상변태 [6] Chemical potential과 Activity/ Activity Coefficient

 

재료상변태 [5] Binary System에서 Ideal solution과 Regular Solution

 

1. Chemical Potential; 물질의 에너지적인 위치

Chemical Potential (화학 퍼텐셜, μ)
: 어떤 물질이 계(system) 안밖으로 이동할 때, 그 물질의 에너지 변화량을 나타내는 값이다. 즉, 물질의 '퍼짐 경향'을 에너지 관점에서 표현한 값이다

 

 

 

깁스 자유 에너지가 물질 i의 몰 수가 아주 조금 바뀔 때 얼마나 변하는지를 나타내는 값이다.

 

 

Chemical Potential이 중요한 이유는 무엇일까?

 

'Chemical Potential'은 물질의 이동이 자발적인지 아닌지 알려준다. Energy Pressure 개념이라고 이해하면 쉬운데, 물질은 퍼텐셜이 높은 곳에서 낮은 곳으로 이동한다. μ(chemical Potential)이 낮은 물질은 물질을 계속 넣어도 △g 가 작기 때문에 ' 방출 경향'이 적다. 즉, 물질을 넣어도 system이 안정적이다.

 

 

반대로, μ(chemical Potential)이 크다는 것은 그 물질을 넣는데 많은 에너지가 필요하다는 뜻이므로, '방출 경향'이 적다고 볼 수 있다.

 

1-1. μ (Chemical Potential)과 Gibbs Free Energy

 재료 상변태에서 두 상의 Gibbs Free Energy가 같을 때 상변태가 일어난다는 것이 바로 핵심 원리이다. 성분이 하나일 때는 상변태 시점 및 조건을 찾기 간단하지만, 성분이 여러개인 합금 처럼 복잡한 경우, 화학 퍼텐셜을 기준으로 그 시점을 정의한다.

 

 

 깁스 자유 에너지 G 공식은 다음과 같다.

이때, H = U+ PV를 넣으면, 아래와 같이 바꿀 수 있다.

위 식을 각 성분에 대해 미분해보자.

 

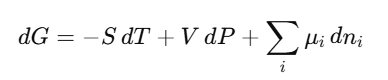
 여기서, Gibbs Free Energy를 물질 i의 몰수 ni에 대해 미분한 것이 바로 '화학 퍼텐셜'이다. 즉, T, P 일정한 조건에서 생각하자면, 화학 퍼텐셜은 몰수의 변화가  '깁스 자유 에너지가 어떻게 바뀌는지'를 알려주는 도구이다.

 

 

 

이를 이용하여 시스템의 변화를 생각할 때 어떻게 쓰는 지 알아보자.

 

시스템이 평형 상태일때	Chemical Potential 값이 같기 때문에 'μA = μB' 이므로, ΔG= 0 을 만족 화학 퍼텐셜이 같아질 때 반응이 멈춘다.
어떤 변화가 자발적으로 일어날때	어떤 반응이 자발적으로 일어나기 위해서는 ΔG < 0이어야 한다.  Ex) 기체가 퍼지는 상황에서 압력이 낮은 쪽이 μ이 낮으므로, ΔG 가 줄어든다. 즉, 자발적 변화가 발생한다.

 

1-2.  Ideal Solution과 Regular Solution에서의 Gibbs Free Energy

 

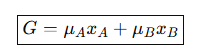
 위 식은 Ideal Solution이나 Regular Solution에서 화학 퍼텐셜과 몰 분율을 곱한 값을 더한 것으로, 혼합물의 몰당 Gibbs Free Energy를 나타내는 값이다. 따라서, 단순히 평균 값이 아닌 가중 평균 형태로 구한 Gibbs Free Energy이다. 이는 각 성분의 화학 퍼텐셜에 그 성분이 전체에서 차지하는 비율을 곱해서 평균을 낸 것이다.

 

 

1-2-1. Ideal Solution

아래 이 두 식을 위의 Gibbs Free Energy 식에 넣어보자.

이제 항을 분배해서 정리해보자. 이제 나온 식은 Ideal Solution에서의 깁스 자유 에너지 공식이다.

 

Ideal Solution에서 Gibbs Free Energy

1-2-2. Regular Solution

 Regular Solution의 화학 퍼텐셜 공식을 위 ideal Solution과 동일한 방식으로 대입해보자.

 

Regular Solution에서의 Gibbs Free Energy

 

 Regular Solution의 경우 Ideal Solution과 달리, △H mix에 대한 항이 추가로 붙는다. 실제 혼합물에서는 단순히 몰분율 개념으로만 설명되는 것이 아닌 상호작용 에너지가 반영되어야 한다. 따라서, 위의 내용을 바탕으로 Activity의 개념이 등장하게 되었다.

 

1-3. Activity의 개념

 

농도가 xi라 하더라도, 실제 혼합에 기여하는 효과는 다를 수 있기 때문에 그 효과만 반영하는 실질적인 농도를 새로 정의한 것이 바로 'Activity'이다. 쉽게 말하자면, '용액 속에서 어떤 성분이 이상 용액처럼 행동하는 정도'를 나타내는 척도이다.

 

​- a_i : 실제 퍼탠셜 변화에 영향을 주는 '효과적인 농도'

- x_i : 명목 상의 농도(실제로 얼마나 들어있는가)

- γ_i : 그 농도가 퍼텐셜에 실제로 얼마나 주는 가? 

 

 

 이상 용액에서는 성분 간 상호작용이 완전히 균일하기 떄문에, 화학 퍼텐셜은 매우 단순하다.

 

 

 

그러나, 현실의 비이상용액에서는 성분 간 상호작용이 균일하지 않기 때문에 그로인해 퍼텐셜이 다르게 움직이게 된다.

이러한 사실을 반영해서 위 Regular Solution의 화학 퍼텐셜을 다시 작성해보면, 다음과 같다.

 

 

Activity가 x_i와 같으면 그 성분은 이상적으로 행동한다. 만일 activity가 x_i보다 크면, 그 성분은 휘발성이 크거나 퍼텐셜이 크며, 작으면 용액에 더 잘 녹아있고 휘발성이 낮다. 따라서, 단순한 농도의 개념이 아닌 실제로 이 성분이 얼마나 활발히 작용하는지를 반영한다.

 

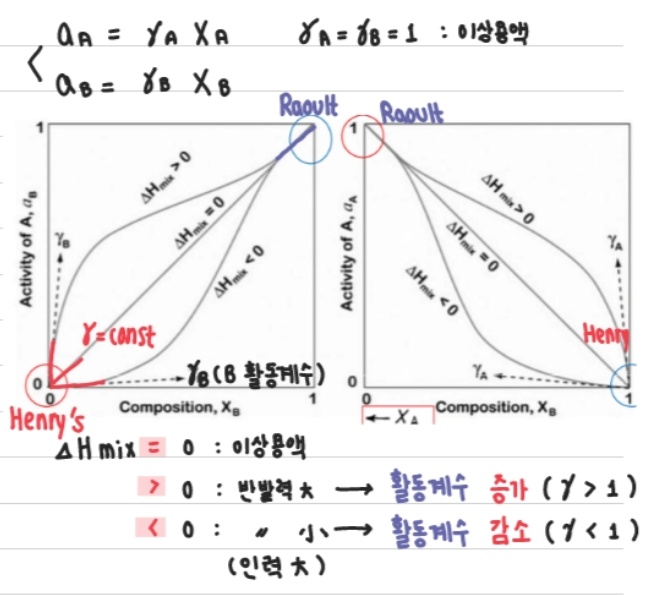
1-4. Raoult's Law와 Henry's Law

 

 우리는 이제 한 가지 질문을 해 볼 수 있다.

 

Activity가 농도에 따라 어떻게 달라질까?

 

 Activity는 이전에 말했듯이 '농도의 함수'이다. 즉, γi가 조성에 따라 달라지면, Activity도 바뀐다.

 

 Ideal Solution (이상용액)에서는  γi = 1로 항상 일정하기 때문에 ai = xi이다. 그러나, Regular Solution의 경우 γi는 몰분율 x_i가 작거나 크면 1에서 벗어나며 x_i가 1의 근처에서는 γi ∽ 1이 되지만, xi 가 0의 근처에서는 Henry's Law를 따른다. 즉, 조성에 따른 Activity가 바뀌는 것을 알 수 있다.

 

 

Ideal Solution	γi​ = 1 → 항상 일정  ⇒ ai ​= xi​
Regular Solution	γi는 몰 분율 xi가 작거나 크면 1에서 벗어난다.	xi→1 → γi ≈ 1
		xi​→0 → γi​는 Henry’s Law를 따른다

 

1-4-1. Raoult's Law ; 용매

 라울의 법칙
:용액중의 성분이 이상적으로 섞인다고 가정할 때, 그 성분의 부분 증기압은 몰분율에 비례한다는 법칙이다.

 

 즉, 성분이 이상적(ideal)으로 섞였으면, 각 성분은 자기 증기압을 몰분율 만큼 기여한다. 따라서, 이상용액에서의 activity ai​=xi​라는 점에서 activity와 연관 지어볼 수 있다. 원점에서 직선을 가지는 형태를 띈다.

 

 

1-4-2. Henry's Law ; 용매

 헨리의 법칙: 용질이 매우 희석된경우, 해당 용질의 부분 증기압은 몰분율에 비례하나, 비례 상수는 고유 상수(Henry's Constant)를 쓴다는 점에서 다르다.

 

이때 헨리 상수는 '용질이 용매 속에서 얼마나 편안한지'를 나타내며, 상수가 크면 휘발성이 높고 작으면 용액에 남으려 한다.  이 법칙은 소량 성분(용질)에 대해 적용하는 법칙이다.