재료상변태 [7] Single/ Binary Phase에서 Equilibrium Condition과 Unlimited Solubility & Ideal Solution 등
재료상변태 [6] Chemical potential과 Activity/ Activity Coefficient
재료상변태 [5] Binary System에서 Ideal solution과 Regular Solution재료상변태 [4] Heat Capacity(열용량), Enthalpy(엔탈피), Entropy(엔트로피), Gibbs Free Energy재료상변태 [3] 열역학 제 0법칙/ 1법칙/ 2법칙/ 3법칙재료
mayunchem.tistory.com
1. 단일 상(Single Phase)에서의 자유 에너지와 확산, 평형 조건
1-1. 단일 상에서 조성이 다를 때 자유에너지의 변화
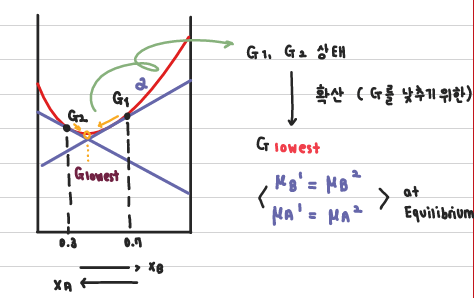
자유 에너지가 가장 낮은 곳이 평형 상태에서 실제로 존재하는 조성이다.
1-2. 혼합에 따른 자유 에너지의 변화; 화학적 퍼텐셜 차이에 의한 확산

Single Phase에서 조성이 다른 G1과 G2 를 섞어보자. 이 둘을 맞닿고 T(온도)를 올리면 확산이 발생한다. 이 둘이 더 낮은 △G를 가지기 위해서는 1번에서는 X_A가 커져야 하고, 2번은 X_B가 커져야 한다.
확산은 Chemical potential이 큰 쪽에서 작은 쪽으로 원자가 이동한다.

Chemical Potential 뿐 아니라, 활동도를 고려해보자.

Chemical Potential이 커지면, 활동도도 커진다. 즉, 활동도가 높은 곳에서 작은 쪽으로 이동한다고 생각 할 수도 있다.

아래 그림에서는 Chemical Potential이 아닌 '활동도 차이'에 의한 확산을 확인할 수 있다.

위의 내용을 요약하자면 다음과 같다.
한 상 안에서 조성 차이로 생기는 μ 차이 → 확산 발생 → μ 같아짐 → 평형 도달
1-3. Mg와 Si의 Solid Solution 생성
두 원소가 단일 상 안에서 자유 에너지 감소를 위해 섞이기 위해서는 결정 구조 적으로도 섞일 수 있어야 한다. 그렇다면, 결정구조가 다른 Mg와 Si는 섞일 수 있을 까?
Mg(HCP 구조)와 Si(Diamond 구조)의 자유 에너지 곡선을 비교해보자.

이 두 가지 원소가 섞이기 위해서는 결정 구조 적으로도 섞일 수 있어야 한다. 단순히 자유 에너지가 낮아진다고 무조건 고체 용액이 형성되는 것이 아니라, 열역학적으로 섞이는게 유리하더라도 결정구조가 다르면 실제로 고용체가 생기기 어려울 수 있다. 만일, 같은 결정구조를 공유하는 경우에는 Solid Solution의 형성이 가능하다.
2. Two Phase에서 Equilibrium Condition
2-1. Gibbs Duhem 식과 공통 접선 조건
열역학 평형의 핵심은 단 하나였다.
' 모든 성분의 화학 퍼텐셜이 두 상 사이에서 같아야 한다.'
Two Phase에서 평형조건은 다음과 같다. A와 B가 둘다 α 상과 β 상에서 각각 μ가 같아야 평형이야.

이 식을, Gibbs-Duhem 식과 결합해보자.
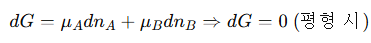
평형이면, 계 전체의 자유 에너지가 더이상 줄어들 수 없어야 하므로 dG = 0을 만족해야 한다. 즉, 두 상 간의 화학 퍼텐셜이 같아야 한다. 이 식을 통해 우리는 각 상의 조성에서 그리는 자유 에너지 곡선에 대해 '공통 접선 조건'을 만족해야 한다는 사실을 알 수 있다. 왜냐하면 G(자유 에너지)의 기울기가 화학 퍼텐셜이기 때문이다.


2-2. Mg와 Si의 Solid Solution 형성과 Phase seperation
; 단일 상이 아닌 분리되는 이유
이때, Mg와 Si를 예를 들어 생각해보자.

Mg와 Si는 이전에 서로 결정 구조가 각각 HCP와 Diamond structure로 각각 다른 것을 확인하였다. 즉, 고용체의 형성이 어렵기 때문에 상 분리가 나타나게 된다.
곡선에서 g 곡선 2개가 따로 존재하고 그 곡선에 공통 접선을 그려서 접점에서의 조성이 xα,xβ가 각각 되며, 그 사이의 조성은 두 상의 공존 영역이 된다.
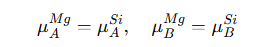
확산과 교환이 일어나면서 Chemical Potential은 평형에 도달하는데, 결정 구조가 다르다면 실질적인 확산 저항이 커지며 한 상으로 혼합되지 못하고 상 분리가 일어나게 되는 것이다.
2-3. Isomorphous Alloy & Hume - Rothery Rule
위에서 단일 상이 생성되지 않고 두 가지의 상으로 분리되는 경우를 살펴보았다.
그렇다면, 반대로 '두 상이 생기지 않고 단일 상이 유지되는 조건은 무엇일까'?
Isomorphous = iso (같은) + morphous (형태)
: 같은 결정 구조를 가지는 합금 시스템을 의미하며, 모든 조성에서 단일 고체 용액을 이루는 합금계를 의미한다.
우리는 단일 상이 생기는 조건을 Hume - Rothery Rule을 통해 알아볼 수 있다.

만일 이 4가지 조건을 만족한다면, 단일 고체 용액이 형성되고 이러한 시스템을 isomorphous alloy라고 한다.
Cu와 Ni의 경우, 동일 FCC 구조를 가지며 아래 4가지 조건을 만족하기 때문에 단일 상을 형성한다.
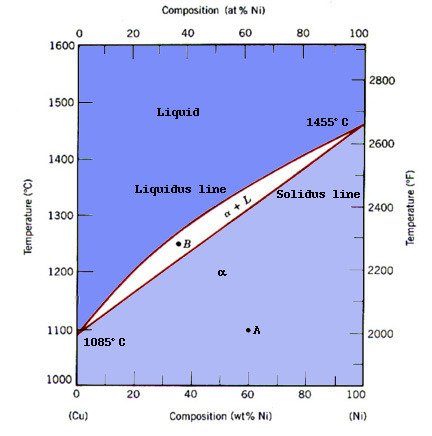
또, Ag - Au Phase Diagram도 이와 동일하다.
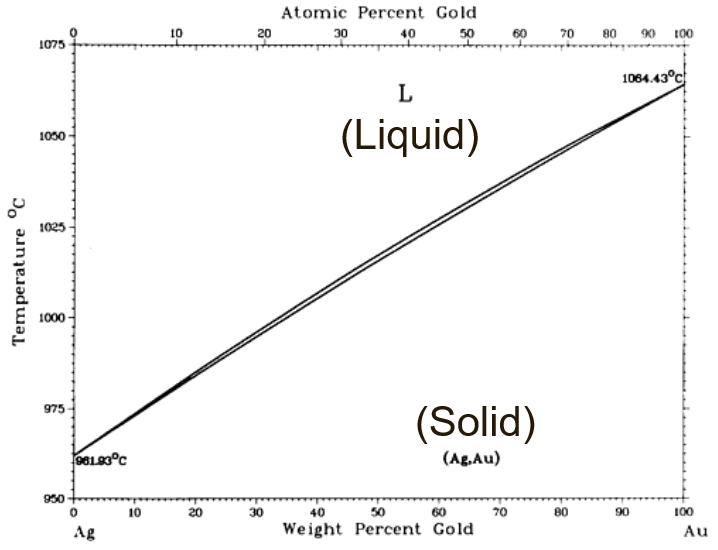
3. Heterogenous System에서 Equilibrium
Heterogenous System
: 서로 다른 상이 공존하는 시스템.
하나의 물질이 아니라 2개 이상의 상이 같은 공간에 동시에 존재하는 경우를 의미한다.

왼쪽 첫번째 그래프를 보면, 자유 에너지를 X축 조성에 따라 그린 곡선에서 α-phase, β-phase 각각의 곡선이 존재한다. 이때, 두 상이 공존 가능한 조성 범위는 공통 접선을 통해 결정된다. (공통 접선 원리)
두 상이 공존할 때 전체 자유 에너지가 최소가 되어야 하며, 활동도와 화학 퍼텐셜이 모두 같아야 한다.

이 그림에서 빨간 자유 에너지 곡선의 위로 불록한 부분은 공통 접선이 그려질 수 없다.(불안정)
단순히 Gibbs Free Energy가 낮은 구간이 아닌 공통 접선을 그었을 때의 기준임을 명시해야한다.
4. Unlimited Solubility & Ideal Solution
위 Heterogenous System에서의 Solubility는 섞이지 않고 상분리가 일어나는 이질계에 대해 다루었다. 공통 접선 법칙을 통해 두 상이 공존하는 영역이 존재함을 확인하였다.
그렇다면, 항상 두 상이 생기는 걸까(이질계)?
혼합되어 단일 상이 존재할 수는 없는 걸까?
경우에 따라 혼합되어 단일상(Single Phase)가 될 수 있다.
이러한 의문에서 등장한 개념이 바로, Unlimited Solubility와 ideal Solution이다.
4-1. Unlimited Solubility
Unlimited Solubility
: 두 원소 A, B가 어느 비율로 섞이든 완전히 서로 녹는 경우
이 경우에는 단일 상이 유지되며, 상 분리가 일어나지 않는다. 대표적인 예로, Cu- Ni, Ag- Au가 있다.
이때 Gibbs Free Energy를 보면 곡선이 볼록해 공통 접선을 그을 수 없다. 이러한 완전한 섞임을 설명하는 개념이 Ideal Solution이다.
4-2. Ideal Solution
Ideal Solution: 두 성분 A, B가 고체, 액체에서 무한히 섞일 수 있는 계를 의미한다.
혼합 엔탈피 = 0이고, 혼합 엔트로피만 작용하기 때문에 혼합이 더 유리해지는 것을 식을 통해 확인할 수 있다.

그래프에서 찾아보자.
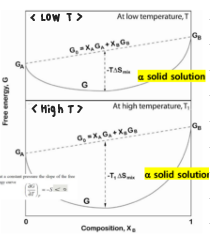
어떤 온도나 조성이든 고용체를 항상 형성하는 모습을 확인 할 수 있다.
Ideal Solutiom과 Isomorphous Alloy는 어떻게 다를까?
Ideal Solution은 이론적 개념(모델)으로, 완전한 무작위 혼합을 가정하고 고온에서 주로 성립하는 '열역학적으로 완벽하게 섞이는 모델'을 의미한다.
Isomorphous Alloy는 현실적인 금속 시스템에서 실제로 나타나는 구조적 개념으로, Hume-Rothery 조건( 같은 결정 구조를 갖고, 원자 반지름, 전기음성도 차이 적음 ) 을 만족할 경우 확인할 수 있다.
5. Δ H mix < 0 (발열 반응) & Δ H mix >0 ( 흡열 반응)
5-1. Δ H mix < 0 (발열 반응)
A와 B가 혼합될 때 열을 방출하는 것으로, A-B간 결합이 A-A 나 B-B보다 더 안정하다는 뜻이다. 즉, 혼합이 자발적으로 일어나고 안정한 상태를 형성하는 것이다.
그래프에서 살펴보자.
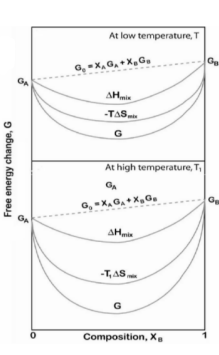
Δ H mix < 0 일때 곡선이 오목하게 휘어지면서 G곡선이 Ideal Solution보다 더 아래로 내려간다.
이렇게되면, 혼합 시 2가지의 양상을 가진다.
첫째는, Solid Solution을 유지한다.
A-B 결합이 좋고, 원자의 크기 차이 등이 모두 적당하면, 그냥 잘 섞이면서 하나의 고체 상을 유지한다.
두번째는, Compound를 형성한다.
A-B 결합이 너무 안정할 경우, 특정 비율에서 고정된 구조의 화합물 (compound)를 형성한다. 예를 들면, Cu-Zn → CuZn, Cu3Zn 같은 금속간 화합물이 생긴다.
즉, 위 내용을 정리해보면
| ΔHmix < 0 | Solid Solution을 형성 |
| ΔHmix <<< 0 | compound를 형성 |
5-2. Δ H mix > 0 (흡열 반응)
이번 경우에는 A와 B가 섞일 때 에너지를 흡수한다는 의미로, 혼합이 에너지적으로 불리한 것이다. 따라서, 물질은 혼합하려고 하지 않고 'Phase Seperation(상분리)' 경향성을 가진다.
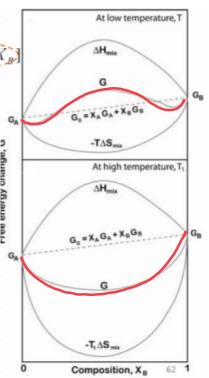
온도가 낮아질 수록 곡선이 납작해지며, 상분리 가능성이 커진다.