재료상변태 [4] Heat Capacity(열용량), Enthalpy(엔탈피), Entropy(엔트로피), Gibbs Free Energy

재료상변태 [3] 열역학 제 0법칙/ 1법칙/ 2법칙/ 3법칙

 

 

1. 열용량(Heat Capacity)

열용량
: 물체가 1 °C만큼 온도가 상승할 때, 필요한 열량(Q)의 양을 의미한다.

 

C: 열용량, Q: 가해진 열량, Δ T: 온도변화

 

위 식을 통해 열용량이 클수록 같은 열량을 가했을 때 온도가 덜 변하고, 열용량이 작을수록 온도가 더 쉽게 변한다.

 

1-1. 정압 열용량(Cp)

: 압력이 일정한 상태에서 1도를 올릴 때 가해지는 열량에 대한 열 용량

 

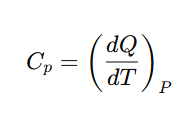
- 기체가 팽창하면서 외부에 일을 하기 때문에, 추가적인 에너지가 필요하므로 Cp > Cv이다.

1-2. 정적 열용량(Cv)

: 부피가 일정한 상태에서 1도를 올릴 때 가해지는 열량에 대한 열용량

 

부피가 일정할 때는 일을 외부에 일을 하지 않는다. 따라서 기체의 내부 에너지만 변화하므로 Cp보다 작다.

 

추가적으로, 고체 상태에서 아래의 식이 성립된다.

 

1-3. 이상기체에서 Cp와 Cv의 관계

 

 

 

2. Enthalpy (H)

엔탈피(Enthalpy, H)
: 계가 보유한 총 에너지를 나타내는 상태함수로, 내부 에너지(U)와 계가 하는 일(PV)의 합으로 정의한다.

 

 

 엔탈피는 상태함수이기 때문에, 화학 반응이나 상태 변화에서 엔탈피의 변화량이 매우 중요하다.

 

dH = dU + PdV(= - W) +VdP = dQ + VdP

 

 

따라서, 등압(P= constant) 에서 계가 흡수하거나 방출하는 열은 엔탈피의 변화와 같다.

 

 

i) ΔH < 0 - 발열 반응
- 반응 중 열이 방출되면 계의 엔탈피가 감소하며 주변 온도가 증가한다.
- ex. 연소 반응, 중화 반응

ii) ΔH > 0 - 흡열 반응
- 반응 중 열이 흡수되면 계의 엔탈피가 증가하며, 주변 온도가 감소한다.

 

 

 

 이상기체에서는 엔탈피의 변화가 정압 열용량과도 관련되어있다. 기체가 등압 조건에서 가열될 때, 엔탈피는 온도와 비례하여 증가한다.

 

따라서 온도에 대한 Enthalpy의 plot는 다음과 같고, 이때의 Slope는 Cp이다.

 

3. Entropy(S)

엔트로피(S)
: 계의 무질서도(Disorder) 또는 가능한 미시 상태의 개수를 나타내는 열역학적 상태 함수이다.

 

 

 엔트로피는 계의 무질서도가 높을수록 증가하며, 가능한 미시상태(Ω)가 많을 수록 엔트로피가 커진다.

 

3-1. 엔트로피의 변화

 엔트로피의 변화는 가역과정에서 계가 흡수된 열을 절대 온도로 나눈 값이다.

 열이 계로 들어오면 (Q>0) 엔트로피가 증가하고, 열이 나가면 (Q < 0) 엔트로피가 감소한다.

 

const P일 경우 dQ = dH = nCpdT이다. 따라서, const P에서 엔트로피도 온도의 함수이다.

온도(T)와 엔트로피(S) 사이의 관계이다

 

 T = 0K에서 Entropy(S)는 0이다.

 

 또한, 이때의 기울기에 대해서 살펴보면, 다음과 같이 나온다. 

 

 따라서, 기울기 Cp/T는 항상 0보다 크며, 온도가 커지며 기울기가 변화한다.

 

4. Gibbs Free Energy

 위의 식을 통해 Gibbs Free Energy의 다양한 형태의 식을 얻을 수 있다.

 

 const P에서 Gibbs Free Energy(G)와 Temperature(T)사이의 관계를 찾아보면,

 

 그래프의 기울기가 - S가 된다. 이때 S(Entropy) 값은 상수 값이 아닌, T에 따라 변하는 값이기 때문에 linear한 형태가 아니라 곡선의 형태로 나온다.

 

 

const P와 T에서 ΔG = Δ H - T ΔS < 0 (Spontaneous)이다.

 

자발적이다는 것이 에너지가 낮아지는 방향이라는 것을 의미할까?

No, 그렇지 않다.
'자유'에너지가 낮아지는 방향이다.

 

 에너지는 여러가지 형태가 존재하는데, 자유/ 내부 에너지 등이 존재한다.

 

ΔG = Δ H - TΔS 

 

이때, ΔH > 0이어도 ΔG < 0일 수 있다. 왜냐하면, TΔS가 양수일수도 음수일 수도 있기 때문이다.

 

4-1. Liquid와 Solid에서의 정압 열용량

이 그래프를 통해 Liquid에서의 Cp가 Solid에서의 Cp보다 항상 크다는 것을 알 수 있다.

 

 이는 열이 소모될 때, 물질은 부피 팽창과 일(W)을 하는데 'Liquid의 부피팽창 > Solid의 부피팽창' 이므로 Liquid에 더 많은 열량을 주어야 한다. 

 

5. Gibbs Free Energy와 Enthalpy

상변태(Phase Transfer)를 할 때의 엔탈피의 변화

Liquid/ Solid에서의 Enthalpy 변화는 다음과 같다.

 

 

 

온도(T) 변화에 따른 G와 H

5-1. Liquid와 Solid 사이의 Gibbs Free Energy의 차이

 

Liquid와 Solid에서의 Enthalpy와 Entropy의 차이는 항상 양수(+) 값을 가진다.

 

 따라서, Temperature(T)에 의해 Gibbs Free Energy가 결정된다. 따라서,  Melting Temperature(M.P)에서 Liquid와 Solid의 Gibbs Free Energy가 같다.

 

 

 

그렇다면, Liquid ↔ Solid에서의 Gibbs Free Energy에 대해 알아보자.

 

△G = G(l) -G(s) 라고 가정해보자.

 

△G = G(l) -G(s) < 0 : Liquid

  → G(l) < G(s) 이므로 Liquid 상태가 더 안정적이다.

 

△G = G(l) -G(s)  > 0 : Solid 이다.

 → G(l) > G(s) 이므로 Solid 상태가 더 안정적이다.

 

 

5-2. 단일 상에서 상의 안정성

Temperature(T)와 Gibbs free energy와 Pressure 사이의 관계

 

 Pressure가 일정할 때, 특정 온도에서 가장 낮은 Gibbs Free energy를 가진 상이 정해지는 것을 알 수 있다. 

 

 

5-3. Clausius clapeyron equation

clausius clapeyron equation
: 물질의 상변화(Phase Transition)에서 평형 증기압과 온도 사이의 관계를 설명하는 열역학식이다.

 

만일 s → l 일 때를 가정해보자.

 

 dG= VdP-SdT 식에서 △G = 0 일때, dG(l) - dG(s) = 0이다.

 

 

Solid → Liquid로 변할 때의 Clausis -Clapeyron Equation을 살펴보자.

클라우지우스 방정식

  

S(s) - S(l)은 항상 음(-)의 값을 가지기 때문에, △V에서 부호로 방정식의 부호가 결정된다.

 

V(s) - V(l)  > 0 이면 방정식은 음의 값을 가지고  V(s) - V(l) < 0 이면 양의 값을 가진다.